Beyond Chance#
Part 2: From Playful Rolls to Universal Order#
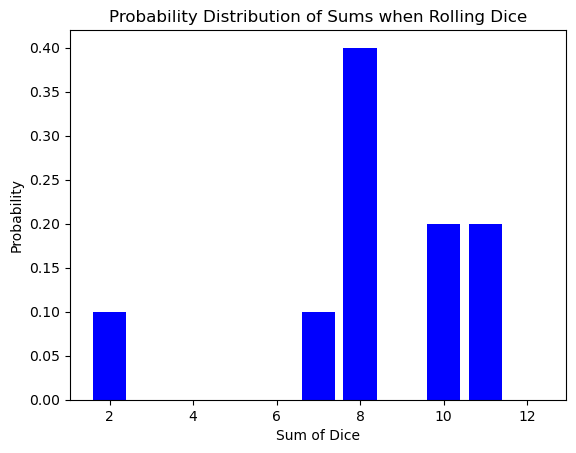
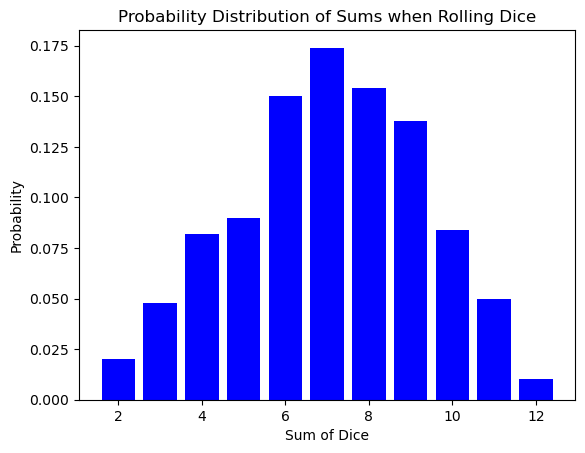
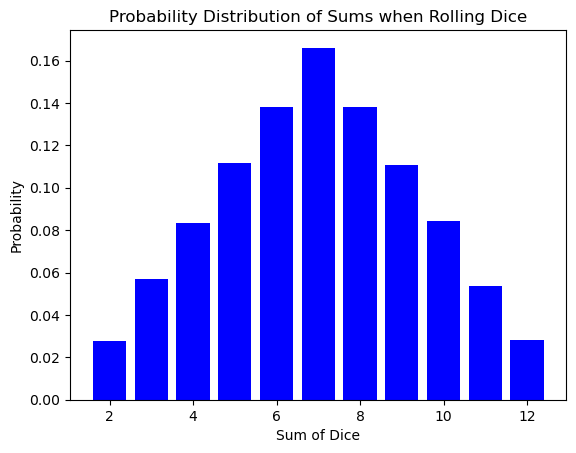
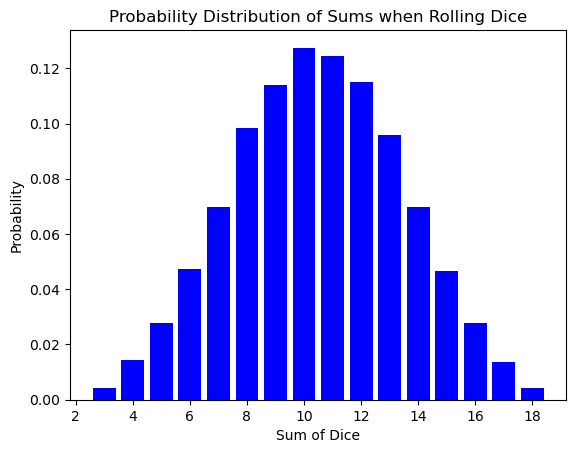
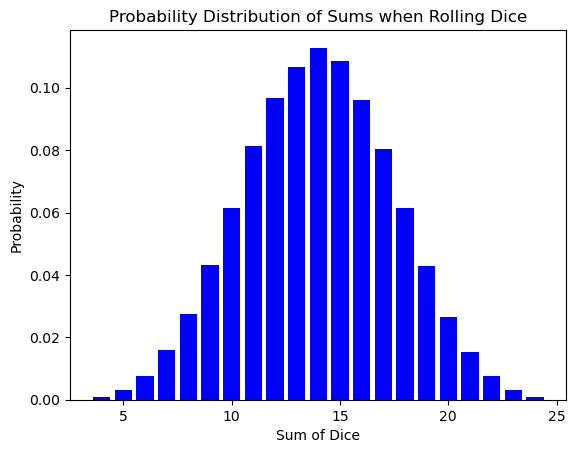
The bell curve of the dice sum distribution might seem like a simple quirk of rolling cubes. However, this very same shape pops up in a completely different arena: the world of atoms and energy!
Thermodynamics, the study of heat, work, and temperature, deals with systems containing a vast number of particles like atoms in a gas. Here, physicist Ludwig Boltzmann discovered that the distribution of energy levels in these tiny particles follows a similar bell-shaped curve. This is known as the Boltzmann distribution for overall energy, which also laid the groundwork for the Maxwell-Boltzmann Distribution. The Maxwell-Boltzmann Distribution takes the Boltzmann principle and applies it specifically to ideal gases. It focuses on the speeds (and related kinetic energies) of individual gas molecules. It tells you the probability of finding a molecule at a particular speed within the container at a specific temperature.
Tip
The Maxwell-Boltzmann distribution describes the speeds of atoms in an ideal gas container at a specific temperature. It’s not a uniform spread – most atoms have speeds around an average value, while fewer have very high or very low speeds. This reflects the range of kinetic energies atoms possess due to their constant motion and collisions. The distribution allows us to predict the probability of finding an atom at a particular speed within the container.
Here’s the exciting part: the number of times you roll the dice is analogous to the number of atoms in a system. Just like a single roll might result in an unlikely outcome (like double sixes), a single atom might have an unusual amount of energy or speed. But as the number of dice rolls increases, the randomness smooths out, revealing the underlying probability distribution.
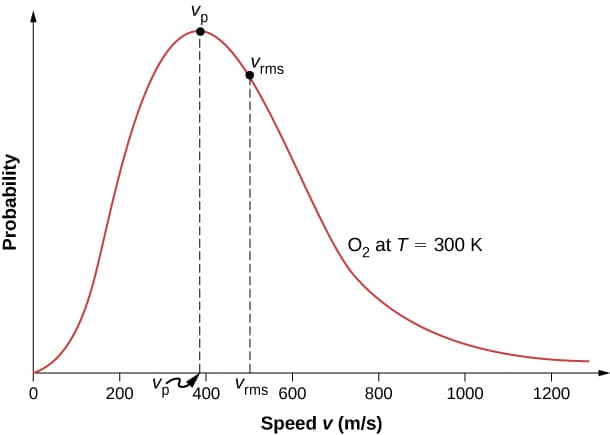
Fig. 1 The Maxwell-Boltzmann distribution of a gas at room temperature, from OpenStax [LMS16]#
Imagine a giant container of gas with countless atoms bouncing around. While we can’t track the individual movements of each atom like we might with a few billiard balls (Newtonian mechanics shines there!), the sheer number of particles makes it impractical. However, probability comes to the rescue! By studying the overall behavior of the gas, like its temperature and pressure, we can use statistical methods (like the ones that govern dice rolls) to understand the average energy distribution of the atoms within.
Similarly, in a vast number of atoms (think Avogadro’s number!), the individual fluctuations in energy average out, and the familiar bell curve emerges. This distribution tells us how likely it is for an atom to have a particular energy level, just like the dice roll distribution tells us the likelihood of getting a specific sum.

Fig. 2 Ludwig Boltzmann (Uni Frankfurt, Public domain, via Wikimedia Commons)#
So, what does this all mean? It means the seemingly random world of dice rolls shares an interesting connection with the microscopic world of atoms. Both are governed by the same underlying principle of probability, where randomness averages out over a large number of events. The next time you pick up some dice, remember, you’re holding a tiny model of the universe, where chance and probability shape reality in fascinating ways.
Bibliography:#
Samuel J. Ling, William Moebs, and Jeff Sanny. University Physics Volume 2. OpenStax, 2016.
Published by Siavash Bakhtiarnia – March 28, 2024